Secondary motions of loom:
The secondary motions of the loom mainly are concerned with moving the fabric through the different parts of the loom. It comprises of taking up and let off motions. The take-up motion helps to wind the cloth onto the cloth roller and also influences the pick density in the cloth. The let-off motion helps to let the warp from the weaver’s beam at a uniform rate thus maintaining the warp tension constant throughout the weaving process. In this article, we will discuss a calculation of secondary motions of loom.

Calculation of Secondary Motions of Loom
Mathematical Problems of Secondary Motions:
Problem-1:
A loom is running with a negative let of motions. The full and empty diameters of the weavers’ beam are 60 cm and 20 cm respectively. The weaver does not want tension variation to exceed 20% during the weaving. How many times the weight has to be shifted during the weaving?
Solution:
We know that,
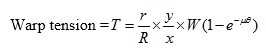
Here full-beam diameter= R1 = 60 cm and empty beam diameter R2 = 20 cm. Let the final tension in the warp is Tf and starting tension in the warp is T1. Tension in the warp varies inversely with the weaver’s beam diameter.
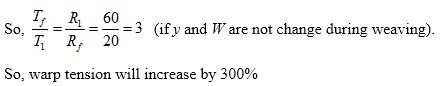
The permissible increase in tension is 20%.
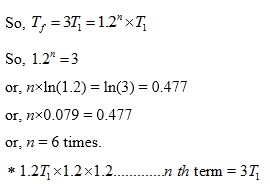
Diameters at which the weight has to be shifted to bring down the tension to T1 are as follows.

So, the weight has to be shifted six times. The last one may be avoided as the beam has become empty (20 cm). (ANS)
You May Like also: Calculation of Weaving Loom Efficiency
Problem-2:
A simple weight lever-based let-off system is attached at each end of a warper’s beam. It is provided with weights of 400 N on each side. The leverage of the system (y/x ratio) is 5:1. The full-beam radius is 50 cm and the ruffle radius is 10 cm. If the ropes are given 1.5 warps around the ruffles and the coefficient of friction is 0.20, determine the warp tension at the slipping point.
Solution:
We know that
Considering two sides of the loom the warp tension will be = 399.2 × 2 = 678.4 N
So, the warp tension at the slipping point is 678.4 N. (ANS)
Problem-3:
A 75 Stockport reed (number of dents / 2 inch) of 1.4 m width is being used on a loom. The reed plan is two ends in a dent. If the weft crimp is 6% then calculate the ends per cm in the fabric on the cloth roller.
Solution:
We know that
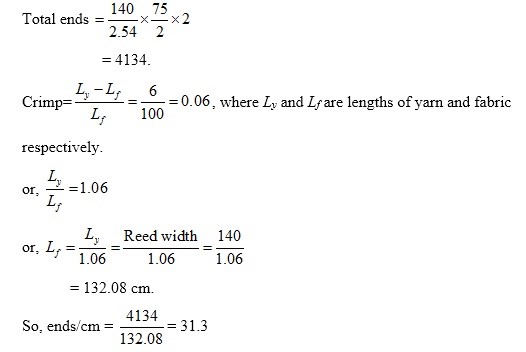
So, ends per cm are 31.3 (ANS)

